퓨리에 변환(Fourier Transform, 푸리에 변환)
푸리에 변환이 맞는 말이라고 한다.
하지만 인터넷을 검색하면 퓨리에 변환 이 더 많은 검색결과를 내준다.
뭐에 쓰는 물건인가?
남자, 여자가 동시에 떠들어 대면 소리가 섞이게 된다.
이런 경우 남자의 소리만 추출하고 싶다면 어떻게 할 수 있을까?
전파의 경우도 원본전파, 잡신호(white noise), 뒤늦게 도착한 원본전파가 섞여 있는 상태이다.
이 때 원본 전파만 얻으려면 어떻게 할 것인가?
이런 섞여 있는 상태의 파동(소리 또는 전파)를 분리해 내는 기능을 하는 것이 퓨리에 변환이다.
푸리에 변환 전계
-
파동은 sin, cos 으로 나타낼 수 있다.
-
모든 파동은 sin, cos의 합으로 이루어져 있으며 역으로 파동을 sin, cos으로 나타낼 수 있다
(푸리에 급수). -
푸리에 급수에서 계수와 주파수를 구한다.
-
이 계수와 주파수가 푸리에 변환이다.
구현
일단 sox 를 이용해 wav 파일을 생성한다.
사람의 가청주파수 때문에 들을 수 있는 주파수는 300Hz, 10000Hz 뿐이다.
sox --null -r 22050 sine_20.wav synth 3 sine 20 #20Hz
aplay sine_20.wav
sox --null -r 22050 sine_300.wav synth 3 sine 300 #300Hz
aplay sine_300.wav
sox --null -r 22050 sine_10000.wav synth 3 sine 10000 #10,000Hz
aplay sine_10000.wav
sox --null -r 22050 sine_30000.wav synth 3 sine 30000 #30,000Hz
aplay sine_30000.wav
sox --combine mix --volume 0.5 sine_300.wav --volume 0.5 sine_10000.wav sine_mix.wav
aplay sine_mix.wav#!/usr/bin/python3
import os
import glob
import scipy
import scipy.io.wavfile
from scipy import fftpack
import matplotlib.pyplot as plt
import numpy as np
def plot_wav_fft(wav_filename, desc=None, trans=False):
plt.clf()
plt.figure(num=None, figsize=(6, 4))
sample_rate, X = scipy.io.wavfile.read(wav_filename)
spectrum = fftpack.fft(X)
freq = fftpack.fftfreq(len(X), d=1.0 / sample_rate)
plt.subplot(211)
num_samples = 300.0
plt.xlim(0, num_samples / sample_rate)
plt.xlabel("time [s]")
plt.title(desc or wav_filename)
plt.plot(np.arange(num_samples) / sample_rate, X[:int(num_samples)])
plt.grid(True)
if trans:
plt.subplot(212)
plt.xlim(0, 5000)
plt.xlabel("frequency [Hz]")
plt.xticks(np.arange(5) * 4000)
if desc:
desc = desc.strip()
fft_desc = desc[0].lower() + desc[1:]
else:
fft_desc = wav_filename
plt.title("FFT of %s" % fft_desc)
plt.plot(freq, abs(spectrum), linewidth=2)
plt.grid(True)
plt.tight_layout()
rel_filename = os.path.split(wav_filename)[1]
plt.savefig("%s_wav_fft.png" % os.path.splitext(rel_filename)[0],
bbox_inches='tight')
plt.show()
def plot_wav_fft_demo():
plot_wav_fft("sine_300.wav")
plot_wav_fft("sine_10000.wav")
plot_wav_fft("sine_mix.wav")
plot_wav_fft("sine_mix.wav", "sine_mix", True)
plot_wav_fft_demo()위 파일을 실행시키면 아래와 같이 주파수 그래프가 그려진다.
300Hz
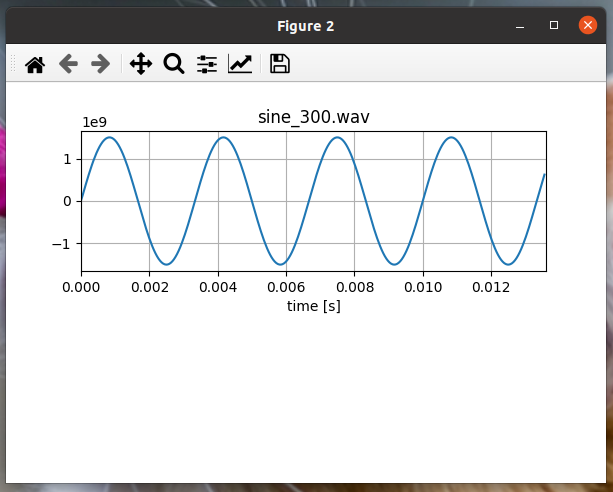
10000Hz
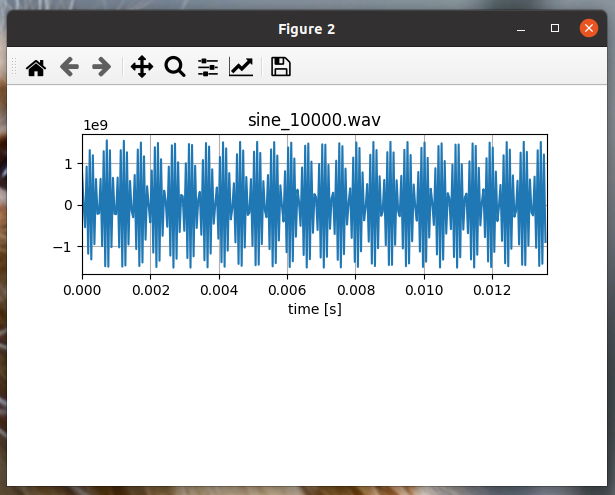
300Hz + 10000Hz
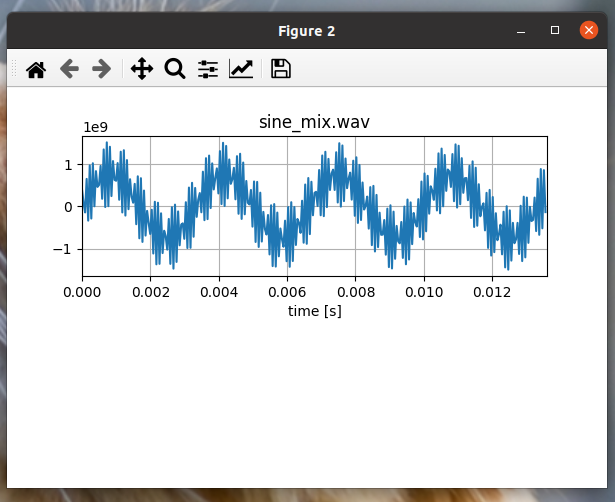
마지막으로 요상한 그래프가 나왔다.
이것이 퓨리에 변환이다.
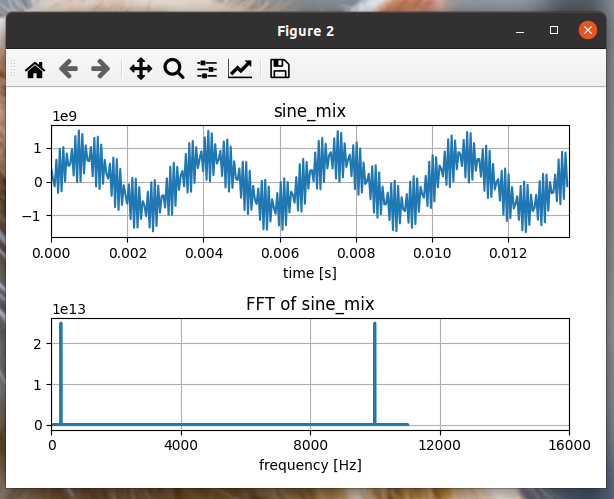
위 두 그래프중 아래 그래프의 X축을 가만히 보면,
300Hz, 10000Hz 처럼 보이지 않는가?
좀 더 확실히 하기 위해,
200Hz 와 300Hz 파일을 생성하고,
볼륨도 0.3, 0.7 로 다르게 입력하고 다시 동일하게 실행시켜 보자.
sox --null -r 22050 sine_200.wav synth 3 sine 200
sox --null -r 22050 sine_300.wav synth 3 sine 300
sox --combine mix --volume 0.3 sine_200.wav --volume 0.7 sine_300.wav sine_mix_200_300.wav# ......................
if trans:
plt.subplot(212)
plt.xlim(0, 20)
plt.xlabel("frequency [Hz]")
plt.xticks(np.arange(5) * 100)
# ......................
def plot_wav_fft_demo():
# plot_wav_fft("sine_200.wav")
# plot_wav_fft("sine_300.wav")
# plot_wav_fft("sine_mix_200_300.wav")
plot_wav_fft("sine_mix_200_300.wav", "sine_mix", True)
plot_wav_fft_demo()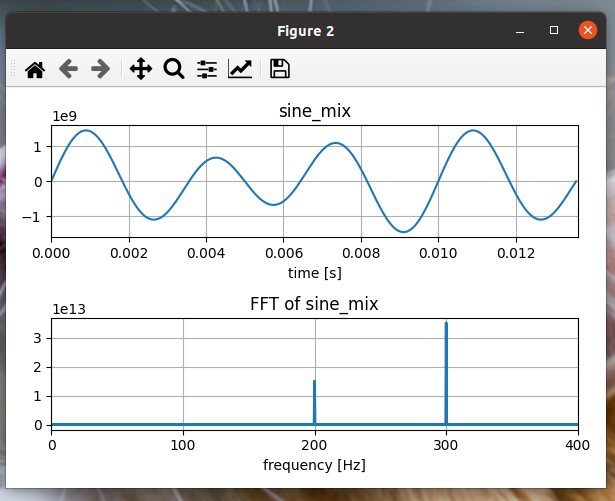
푸리에 급수(Fourier series)
푸리에의 발견 : 동일한 형태를 반복하는파동은,
아무리 복잡한 것이라도 단순한 파동의 조합이다.
위에서 보았듯이 200Hz + 300Hz 의 주파수가 복잡해 보이지만,
결국 단순한 파동 두가지가 섞여서 나오는 것과 같다.
이것을 수식화 해보자.
(복잡한 파동) = (단순한 파동 1) + (단순한 파동 2) + (단순한 파동 3) + ...이를 수식화하면 아래와 같은 공식이 나온다.
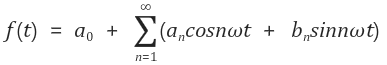
퓨리에 변환
퓨리에 급수가 주기를 가지는 파동의 주파수 요소를 찾는 것에 비해,
퓨리에 변환은 현재 보이는 파동이 무슨 주파수로 구성되어 있는가를 찾는다.
이 아이디어가 엄청난 결과를 만든다.
퓨리에 변환의 응용
소리 영역에 대해서는 mp3, 영상 영역에서는 mpeg/jpeg 등.
정말 많은 곳에서 쓰이고 있다.
퓨리에 급수가 주기를 가지는 파동의 주파수를 찾는건데…
그런거 다 필요없고 그냥 지금의 파동이 무슨 주파수로 이루어 졌냐만 찾는 개념이다.
최근 0.1초의 데이타가 복잡한데…
이걸 퓨리에 변환으로 바꾸면 데이타가 엄청 줄어드는 느낌이랄까…
퓨리에 변환 = 전파 세계에서 알파이자 오메가
아직 공부가 부족하지만,
주파수를 분리해 내고 신호의 강도를 분리해 내는걸 보면,
전파에 대해 얼마나 퓨리에 변환을 써먹으려 했을지 않봐도 비디오고,
나도 그랬을거고,
실제로도 그럴것 같다.