단순 선형 회귀(simple linear regression)

아파트 평수라는 단하나의 특성(feature) 으로 아파트의 가격을 예측한다고 할 때, 아래와 같은 가설(Hyperthesis) 을 세울 수 있습니다.

참조 : Katex

H(x) = Wx + b

위 수식에서 W 는 가중치(Weight) 가 되고, b 는 절편(bias) 이 됩니다.

아파트 가격 예측

서울시에 있는 임의의 10채의 아파트의 평수와 매매가를 구해 시각화해 보았습니다.

import numpy as np
from matplotlib import pyplot as plt

data = np.array([[212, 10.75],
                 [152, 12.9],
                 [158, 12.0],
                 [202, 13.5],
                 [106, 9.5],
                 [181, 11.8],
                 [80, 6.7],
                 [152, 12.8],
                 [88, 8.8],
                 [158, 11.8]])

plt.scatter(data[:, 0], data[:, 1])
plt.title("Area / Price")
plt.xlabel("Price (million won)")
plt.ylabel("Area (square meter)")
plt.axis([0, 420, 0, 50])
plt.show();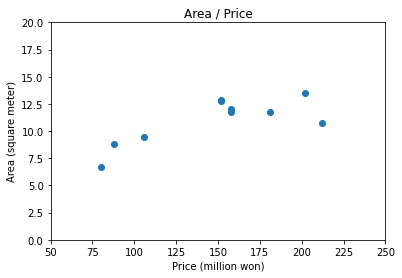

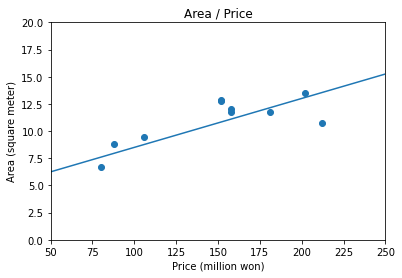
대강 아래와 같은 1차 함수가 평균치가 될 듯 합니다.

비용(cost) 함수

실제값과 예측값의 오차(error) 를 측정하는 함수를 비용(cost) 함수 라고 합니다.

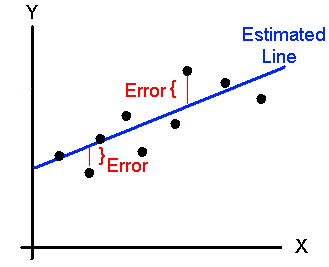
가장 많이 쓰이는 함수가 MSE(Mean Squared Error) 입니다. 오차제곱의 평균을 구하는 방식입니다.

MSE = \cfrac 1 n \displaystyle\sum_{i=1}^n(y_i - \tilde{y_i})^2

가중치 W 를 변경하면서 오차가 최소가 되는 W 를 구할 수 있습니다.

J = \cfrac 1 n \displaystyle\sum_{i=1}^n(pred_i - y_i)^2

예측값과 실제값과의 차이를 제곱하고 합산한 후 평균을 내어 그 비용을 최소화하는 W 값을 구하면 됩니다.

경사하강법

MSE 는 오차를 제곱하는 방식이기 때문에 W 가 변화할 때, 아래처럼 2차원 곡선이 됩니다.

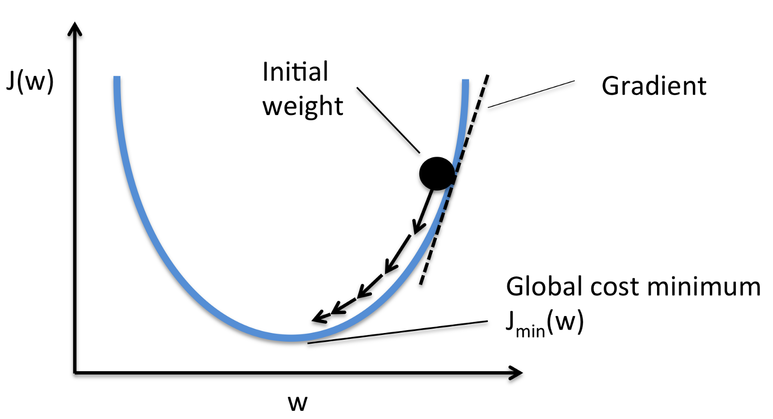
경사가 낮아지는 방향으로 W 값에 변화를 주면서 오차를 줄이는 방식을 경사하강법 이라고 합니다.

W 에 변화를 주는 정도를 학습률(learning rate) 이라고 합니다. 학습률을 너무 작게 하면 너무 오랜 계산시간이 들고, 반대로 너무 큰 값을 할당하게 되면 최적의 W 값을 지나쳐 버리기 때문에 적절한 학습률을 부여해야 합니다.

파이썬으로 구현하기

sklearn 라이브러리를 이용해 구현해 봅니다.

from sklearn.linear_model import LinearRegression
import pandas as pd
import numpy as np

data = np.array([[212, 10.75],
                 [152, 12.9],
                 [158, 12.0],
                 [202, 13.5],
                 [106, 9.5],
                 [181, 11.8],
                 [80, 6.7],
                 [152, 12.8],
                 [88, 8.8],
                 [158, 11.8]])

df = pd.DataFrame({'Area': data[:, 0], 'Price': data[:, 1]})

X = df["Area"]
y = df["Price"]

line_fitter = LinearRegression()
line_fitter.fit(X.values.reshape(-1,1), y)

line_fitter.predict([[200]])
# array([12.91089751])

평수와 가격을 각각 X, y 에 입력합니다.

200 제곱미터의 매매가는 12.9 억으로 예측되는군요.